Probably the most widely used value in a soil report is soil bearing capacity. The obvious reason is that basic examples given in most text books almost always use bearing capacity to calculate the plan dimension of a footing. Because of simplicity and ease of use, this method is still the fundamental soil parameter for foundation design. However, that simplicity assumes the footing will behave as a rigid body. That particular assumption works well in practice for small and single column footings. But for large and multi column foundations, most engineers prefer flexible analysis. Manual computation of flexible analysis could be challenging and, in almost all cases, software programs such as STAAD, SAFE, GT STRUDL etc. are used. However, these computer programs often ask for an input called “modulus of subgrade reaction”. Many engineers are not familiar with this term and often try to compare it with bearing capacity. As more and more engineers will use software to design foundations, it is essential for engineers to have a fundamental understanding of this soil parameter. Is there any relationship between bearing capacity and modulus of subgrade reaction?
Modulus of Subgrade Reaction (Ks)
This term is measured and expressed as load intensity per unit of displacement. For the English unit system, it is often expressed in kip/in2/in; in the SI system it is expressed as kN/m2/m. Some express this term in kip/in3 (or kN/m3) which can be misleading. Numerically, kip/in3 is correct but does not properly represent the physical significance of the measured value and could be mistaken as a density unit or a volumetric measurement.
Mathematically, the coefficient of subgrade reaction is expressed as:
Ks = p/s (Eqn 1)
where p = contact pressure intensity and s = soil settlement
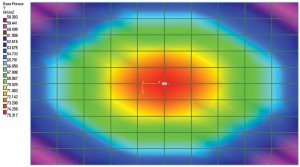
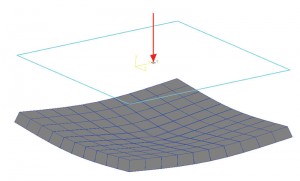
As Terzaghi mentioned, proper estimation of contact pressure for a flexible foundation could be very cumbersome, so it is assumed that Ks remains constant for the entire footing. In other words, the ratio between pressure and settlement at all locations of a footing will remain constant. So the displacement diagram of a footing with a load at center will have a dishing effect. A point at the center of the footing will experience the highest displacement. Displacement reduces as it moves away from the center. Figure 1a shows a simple slab-on-grade foundation. It was modeled and analyzed in STAAD Foundation as “Mat”, which is a flexible foundation; the soil was defined using coefficient of subgrade reaction. For this exercise, the software default value for the modulus of subgrade reaction was used. The displacement diagram shows a dishing effect as discussed earlier. Figure 1b shows the soil pressure contour. It is also obvious that the pressure intensity at the center is maximum and reduces as the elements (or node coordinates) move away from the center. So, it could be assumed that the ratio of pressure intensity and settlement is constant.
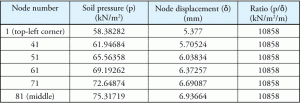
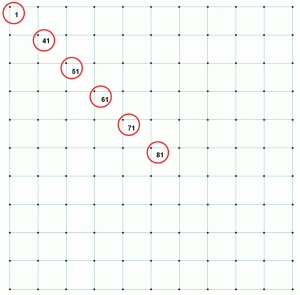
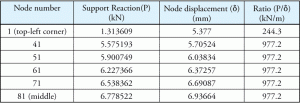
Consider some of the numbers from the same example. Soil pressure, corresponding displacement and the ratio are listed in Table 1. The points are represented on a diagonal to illustrate the variation of pressure and displacement as the points move away from the center to the most distant point in the corner of the rectangular footing. Figure 2 shows the points on the mat slab.
This is hardly a surprise as, by definition, the modulus of subgrade reaction (Ks) is a constant for the entire footing and the program used Ks as its soil property. It is also important to note that the software default Ks value (10858 kN/m2/m) was exactly the same as the constant ratio calculated in Table 1.
Base pressure was calculated from the support reaction. One might think that the ratio of support reaction and corresponding displacement will also be a constant. As shown in Table 2, the ratios are not constant for all values. How is the Ks value used inside the program and how is the base pressure calculated?
Tributary Area
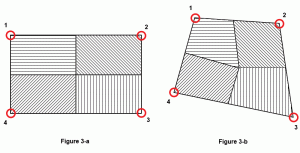
Often an assumption is made to calculate how much area of a plate can be attributed to a node or, in other words, the influence of each node on the surface area of a plate. It depends on the shape of the plate. For a perfect square or rectangular plate, each node will influence exactly ¼ of the plate surface area (Figure 3a). But for a generalized quadrilateral, the best practice would be to calculate the center of the mass of the plate and then draw lines from that center point to the middle points of each side. In Figure 3b, the shaded area represents the influence surface area of the corresponding node.
Spring Support Constant
The above described tributary area calculation is the key procedure used internally by the commercial software to calculate the linear spring constant. The program first calculates the tributary area for each node of the footing and then multiplies the modulus of subgrade reaction by the corresponding tributary area for each node to get the linear spring constant at each node.
Kyi = Ks x Tai (Eqn 2)
where
Kyi is the spring constant at ith node
Tai is the influence area of ith node
Ks is the modulus of subgrade reaction
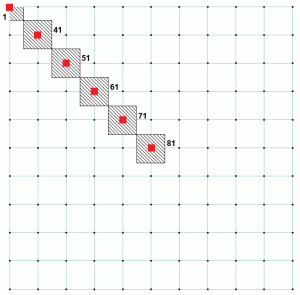
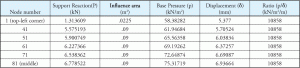
For a concrete foundation analysis, those springs have to be defined as compression-only, as concrete is assumed not to carry any tensile force. The base pressure is calculated at each support node by dividing the support reaction with the corresponding node tributary area. If we look at the above example, Node 1 has a much smaller tributary area than the rest of the nodes. It can also be noted that all other nodes have same tributary area. This explains Table 2, as it shows the ratio for Node 1 is different than other nodes. Figure 4 shows the tributary area for different nodes. Node 1 has a tributary area which is 25% of Node 81. Table 3 is an extension of Tables 1 and 2 and shows how constant ratio is achieved for all nodes.
Allowable Settlement
Bearing capacity is the measurement of the soil pressure a soil can safely bear. In other words, bearing capacity is the pressure which soil can withstand before it fails. The two most important soil failure criteria are:
- Shear failure
- Maximum allowable settlement
Among many factors, foundation width (B) can influence failure criteria. Normally, shear failure governs for smaller foundations and settlement failure governs bigger foundations. Table 4 is a typical example which shows the relationship among different foundation sizes and failure criteria.
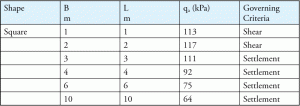
Table 4: Final allowable bearing capacity for allowable settlement = 25 mm and a given embedment depth.
To estimate settlement failure, an allowable settlement value is assumed (normally 25 mm or 1 inch). When soil settles more than the allowable value, the soil fails. So, even for a bearing capacity calculation, an allowable soil settlement is used and structural engineers should be aware of that value while designing a footing. The allowable soil settlement value is typically an integral part of any soil report.
Why Use the Modulus of Subgrade Reaction
It was previously stated that to design a flexible mat foundation, the modulus of subgrade reaction is used instead of bearing capacity of soil. But why? The answer lies in the underlying assumptions of how a foundation might behave.
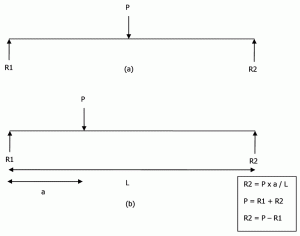
Foundations can be rigid or flexible. Bearing capacity is used to design rigid foundations, but subgrade reaction is used for flexible foundations. The very assumption of a rigid foundation is that “the distribution of the subgrade reaction p over the base of the foundation must be planar, because a rigid foundation remains plane when it settles.” Consider a simply supported beam loaded at its center, as shown in the Figure 5a. By statics, we can obtain R1 = P/2 and R2 = P/2. If the same beam is loaded eccentrically, the reaction can be calculated as shown in Figure 5b.
The same concept is extended for rigid foundation design. But instead of the end supports, the whole foundation is supported. It is also assumed that the relative stiffness of the concrete slab is much higher than the soil stiffness. So, the slab is assumed to remain planar even after the application of load.
Figure 6a shows a footing loaded at the center. From a rigid wide beam analogy, P = R x L. Similarly, for an eccentrically loaded footing, the reaction will vary linearly from one end to the other as shown in Figure 6c. Equations 3 and 4 can be solved to find end reactions. But none of the equations contain modulus of subgrade reaction (Ks). So, the “distribution of subgrade reaction on the base of a rigid footing is independent of the degree of compressibility of the subgrade” it is resting on. As many authors have concluded, a rigid foundation can be safely designed using bearing capacity, as in most cases this method yields more conservative results.
P = 1/2L(R1 + R2) (Eqn 3)
P x a = 1/6B2R1 + 1/3B2R2 (Eqn 4)
But a mat foundation is often designed as a flexible foundation as it can be large in size and there may be many load application points and other complexities, including holes and grade beams. Widespread availability of FEA software contributes to this trend. But, unlike rigid foundations, a flexible foundation cannot have linear subgrade reaction. Rather, it depends on the compressibility of the foundation as well as the structural rigidity. A flexible foundation is subjected to internal bending and relative displacements between two slab points. The greater the structural rigidity, the less the relative displacement. The author tested the case with very high rigidity of the slab elements, resulting in a nearly planar surface after the application of the load. Similarly, the greater the modulus of subgrade reaction, the less the pressure distribution. In other words, a higher Ks value will absorb more pressure at the load application point. Hence, the modulus of subgrade reaction, which is the function of soil settlement and the external pressure,is used for flexible foundation design.
Correlations
The most common – and probably the safest – answer to the question of correlation between bearing capacity and the modulus of subgrade reaction is that there is no correlation. But there should be one, as both are the measurements of soil capacities and any of these two parameters can be used to design a regular foundation.
Again, the definition of Ks is the pressure per unit settlement. In other words, soil capacity to withstand pressure for a given displacement. From earlier discussions, it is also clear that even bearing capacity has an allowable settlement. It is therefore tempting to conclude that the modulus of subgrade reaction is the bearing capacity per unit settlement.
This conclusion is very similar to the equation presented by Bowles.
SI: Ks = 40(SF)qa kN/m3 (Eqn 5)
FPS: Ks = 12(SF)qa k/ft3 (Eqn 6)
where SF = Safety factor and qa is the allowable bearing capacity.
In Equations 5 and 6, the allowable bearing capacity is first converted to ultimate bearing capacity by multiplying with a safety factor. The author assumed one inch or 25 mm settlement. The final equation is then formulated dividing the ultimate bearing capacity by the assumed settlement.
The more generic form of the equation can be written as:
Ks = [pmath]{Iq_a}/delta[/pmath] stress/displacement (Eqn 7)
where
I = Safety factor
qa is the allowable bearing capacity
[pmath]delta[/pmath] is the allowable soil settlement
These equations clearly indicate that the appropriate safety factor must be used, and the Ks value can be better compared with ultimate bearing capacity rather than the allowable bearing capacity. The safety factor can vary depending on projects and geotechnical engineers. The other important factor is the assumed allowable settlement for the calculated bearing capacity.
Similarly, it is to be noted that the base pressure values reported by FEA analysis cannot be directly compared with the bearing capacity. Maximum base pressure should be multiplied by the safety factor and then compared with the allowable bearing capacity of the soil.
However the above mentioned equations have limitations. They can be applied to footings where settlement failure governs, but cannot be related to footings where shear failure occurs before reaching the allowable settlement limit. So, engineers must exercise caution before using these equations.
Conclusion
The correlation between bearing capacity and modulus of subgrade reaction is at best an estimation. It can be used for estimation, but a Ks value determined by a plate load test should always be used if available or should be requested whenever possible. However, the above discussion gives insight into these values and helps engineers to understand the physical significance of modulus of subgrade reaction. And, as always, structural engineers should consult a geotechnical engineer professional prior to finalizing soil stiffness and bearing values.▪
References
Soil Mechanics in Engineering Practice (Third Edition) – Terzaghi, Peck, Mesri
Foundation Analysis and Design (Fifth Edition) – Joseph E. Bowles